How To Calculate Probability Of Drawing Cards

Hypergeometric Distribution Definition

In the statistics and the probability theory, hypergeometric distribution is basically a distinct probability distribution which defines probability of k successes (i.east. some random draws for the object drawn that has some specified feature) in n no of draws, without any replacement, from a given population size Due north which includes accurately K objects having that feature, where the draw may succeed or may fail.

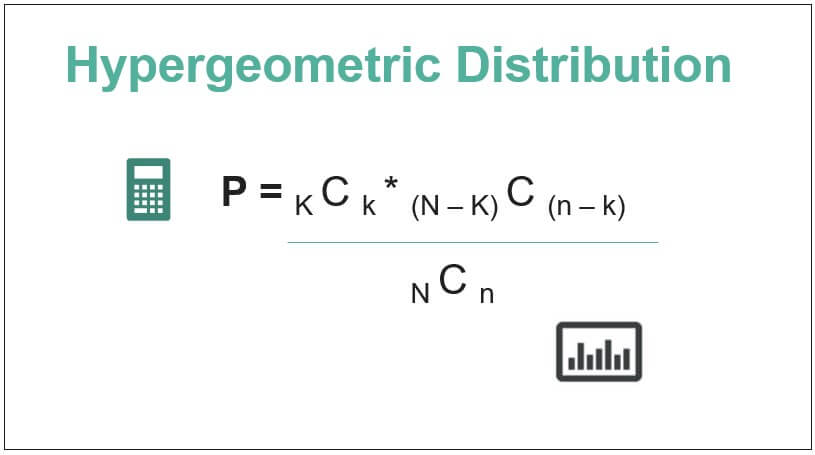
The formula for the probability of a hypergeometric distribution is derived using a number of items in the population, number of items in the sample, number of successes in the population, number of successes in the sample, and few combinations. Mathematically, the probability is represented as,

P = _M C _yard * _{(North – K)} C _{(n – k)} / _N C _n

You are free to use this image on your website, templates etc, Please provide us with an attribution link Commodity Link to be Hyperlinked
For eg:
Source: Hypergeometric Distribution (wallstreetmojo.com)

where,

• N = No. of items in the population
• due north = No. of items in the sample
• Grand = No. of successes in the population
• thousand = No. of successes in the sample

The mean and standard difference of a hypergeometric distribution is expressed as,

Hateful = northward * 1000 / N

Standard Departure = [due north * 1000 * (N – K) * (N – north) / {N² * (North – 1)}]^1/two

Explanation

Follow the below steps:

1. Firstly, determine the total number of items in the population, which is denoted by N. For example, the number of playing cards in a deck is 52.
2. Next, determine the number of items in the sample, denoted by n—for case, the number of cards drawn from the deck.
3. Next, determine the instances which will be considered to exist successes in the population, and it is denoted by Yard. For example, the number of hearts in the overall deck, which is 13.
4. Next, make up one's mind the instances which will be considered to be successes in the sample drawn, and it is denoted past k. Eastward.g., the number of hearts in the cards drawn from the deck.
5. Finally, the formula for the probability of a hypergeometric distribution is derived using a number of items in the population (step 1), number of items in the sample (step 2), number of successes in the population (stride 3) and number of successes in the sample (stride iv) as shown below.

P = _G C _g * _{(Due north – K)} C _{(north – k)} / _N C _n

Examples of Hypergeometric Distribution (with Excel Template)

You tin can download this Hypergeometric Distribution Excel Template here – Hypergeometric Distribution Excel Template

Example #1

Let the states take the case of an ordinary deck of playing cards course where 6 cards are drawn randomly without replacement. Make up one's mind the probability of drawing exactly 4 cherry suites cards, i.east., diamonds or hearts.

• Given, N = 52 (since there are 52 cards in an ordinary playing deck)
• n = six (Number of cards drawn randomly from the deck)
• K = 26 (since there are thirteen red cards each in diamonds and hearts suite)
• thou = 4 (Number of blood-red cards to be considered successful in the sample drawn)

Solution:

Therefore, the probability of drawing exactly 4 red suites cards in the fatigued half dozen cards tin be calculated using the to a higher place formula equally,

Probability = _K C _grand * _{(Northward – Chiliad)} C _{(northward – grand)} / _N C _north

= ₂₆ C _iv * _{(52 – 26)} C _{(half-dozen – 4)} / ₅₂ C ₆

= ₂₆ C _iv * ₂₆ C _ii / ₅₂ C ₆

= 14950 * 325 / 20358520

The probability will exist –

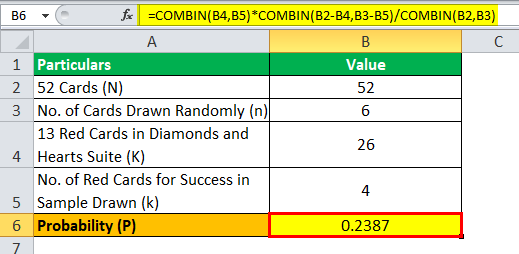
Probability = 0.2387 ~ 23.87%

Therefore, there is a 23.87% probability of drawing exactly 4 red cards while drawing 6 random cards from an ordinary deck.

Case #2

Allow us have some other instance of a wallet that contains v $100 bills and 7 $1 bills. If iv bills are called randomly, so determine the probability of choosing exactly 3 $100 bills.

• Given, N = 12 (Number of $100 bills + Number of $1 bills)
• due north = four (Number of bills chosen randomly)
• Chiliad = v (since in that location are 5 $100 bills)
• grand = iii (Number of $100 bills to exist considered a success in the sample chosen)

Solution:

Therefore, the probability of choosing exactly three $100 bills in the randomly called 4 bills tin be calculated using the higher up formula as,

Probability = _K C _k * _{(Due north – K)} C _{(n – g)} / _N C _n

= _five C _iii * _{(12 – v)} C _{(iv – three)} / ₁₂ C ₄

= ₅ C ₃ * _vii C ₁ / ₁₂ C ₄

= 10 * 7 / 495

Probability volition be –

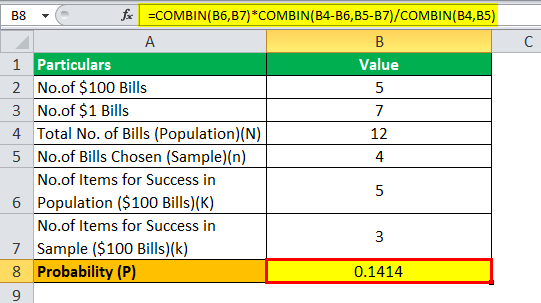
Probability = 0.1414 ~ 14.14%

Therefore, there is a 14.xiv% probability of choosing exactly three $100 bills while drawing 4 random bills.

Relevance and Uses

The concept of hypergeometric distribution is important because it provides an accurate way of determining the probabilities when the number of trials is not a very big number and that samples are taken from a finite population without replacement. In fact, the hypergeometric distribution is coordinating to the binomial distribution The Binomial Distribution Formula calculates the probability of achieving a specific number of successes in a given number of trials. nCx represents the number of successes, while (i-p) n-x represents the number of trials. read more , which is used when the number of trials is essentially large. Withal, hypergeometric distribution is predominantly used for sampling without replacement.

Recommended Manufactures

This article has been a guide to Hypergeometric Distribution Formula. Hither we discuss how to calculate the probability of hypergeometric distribution in excel with examples and a downloadable excel template. You can acquire more about excel modeling from the following manufactures-

• Poisson Distribution
• Bill of Sale
• Formula of T Distribution
• Formula of Standard Normal Distribution
• Deferred Interest

Source: https://www.wallstreetmojo.com/hypergeometric-distribution/

Posted by: bidwellbitheirstake.blogspot.com

Share this post